![]()
Content description
Define congruence of plane shapes using transformations (ACMMG200)
Elaborations
- understanding the properties that determine congruence of triangles and recognising which transformations create congruent figures
- establishing that two figures are congruent if one shape lies exactly on top of the other after one or more transformations (translation, reflection, rotation) and recognising that the matching sides and the matching angles are equal.
Source: Australian Curriculum, Assessment and Reporting Authority (ACARA)
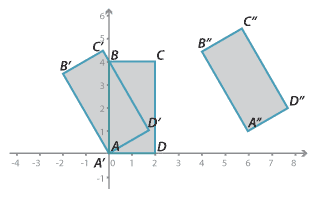
Congruent rectangles
The three rectangles shown above are congruent.
- Rectangle \(A^\prime B^\prime C^\prime D^\prime\) is the image of rectangle \(ABCD\) under a rotation of 30 ° about point \(A\).
- Rectangle \(A^{\prime\prime} B^{\prime\prime} C^{\prime\prime} D^{\prime\prime}\) is the image of rectangle \(A^\prime B^\prime C^\prime D^\prime\) under a translation of 6 units in the positive direction of the x-axis and 1 unit in the positive direction of the y-axis.